概率论和统计学
1、什么是概率论和统计学?它们在数据科学和机器学习中的作用是什么?
概率论和统计学是数学中重要的分支,用于研究随机事件和数据的分布、关联性以及不确定性。
概率论是研究随机事件发生的可能性和规律的数学学科。它提供了一套工具和方法来描述和分析随机变量、随机过程以及他们之间的关系。概率论包括概率分布、随机变量、条件概率、期望值等基本概念,并通过概率模型和统计推断来预测和解释随机现象。
统计学是一门研究收集、分析和解释数据以作出推断和决策的学科。统计学涉及数据的收集、汇总、可视化和推理分析,借助概率论中的概念和方法来建立和验证统计模型,并从样本中推断总体的特征和关系。统计学包含描述统计、推断统计、假设检验、回归分析等内容,旨在通过对数据的分析来获得洞察和决策支持。
在数据科学和机器学习中,概率论和统计学扮演着重要的角色:
- 描述和推断数据:概率论和统计学提供了描述和分析数据的方法。概率分布描述了数据的分布特征,统计推断则使用样本数据进行参数估计和假设检验,以推断总体的特征。
-
建立模型:概率论和统计学提供了建立概率模型的理论基础。通过对数据进行建模,可以从统计角度解释数据的生成过程,并用模型来进行预测、分类、聚类等任务。
-
评估和优化模型:概率论和统计学提供了评估模型好坏的指标和方法,如最大似然估计、贝叶斯推断等。这些方法能够帮助我们从数据中学习模型的参数,优化模型的性能,并对模型进行比较和选择。
-
处理不确定性:概率论和统计学处理不确定性的能力使其在机器学习中发挥重要作用。机器学习算法通常面临不完整或噪声数据,概率论和统计学提供了对这些问题进行建模和处理的工具,如贝叶斯网络、高斯过程等。
综上所述,概率论和统计学在数据科学和机器学习中被广泛应用,它们提供了分析数据、建立模型、优化算法以及量化不确定性等方面的基础和方法,帮助我们从数据中提取知识、做出决策并解决实际问题。
2、概率的基本概念,例如事件、样本空间、概率分布和随机变量。
以下是关于概率的基本概念的详细解释:
1. 事件(Event):
事件是指可能发生或不发生的结果或现象。在概率论中,事件可以是单个结果,也可以是一组相关的结果。例如,掷一个骰子,事件可以是骰子落在特定数字上的结果,或者是骰子落在奇数的结果。
2. 样本空间(Sample Space):
样本空间是指所有可能结果的集合。它代表了一个试验或随机现象的所有可能结果。使用大写字母S来表示样本空间。例如,对于一个掷骰子的试验,样本空间可以是{1, 2, 3, 4, 5, 6}。
3. 概率分布(Probability Distribution):
概率分布描述了随机变量取不同值的概率。随机变量可以是离散的(只能取某些特定值)或连续的(可以取任意值)。概率分布可以用函数、图表或表格来表示。常见的概率分布包括离散分布(如二项分布、泊松分布)和连续分布(如正态分布、指数分布)。
4. 随机变量(Random Variable):
随机变量是定义在样本空间上的变量,它的取值由试验结果决定。随机变量可以是离散的或连续的,并且可以有不同的概率分布。离散随机变量只能取特定的值,而连续随机变量可以在一定范围内取任意值。
随机变量可以分为两种类型:
- 离散随机变量:它只能取一些特定的值,例如投掷硬币的结果(正面或反面)、骰子的点数等。
-
连续随机变量:它可以在一定范围内取任意值,例如身高、温度等。连续随机变量通常由概率密度函数(Probability Density Function, PDF)来描述其概率分布。
以上是关于概率的基本概念的详细解释。这些概念是概率论的基础,用于描述和分析随机事件和现象,并为建立概率模型和进行统计推断提供了理论基础。
3、什么是概率密度函数(Probability Density Function,PDF)和累积分布函数(Cumulative Distribution Function,CDF)?它们有什么作用?
概率密度函数(Probability Density Function,PDF)和累积分布函数(Cumulative Distribution Function,CDF)是描述概率分布的两个重要概念。
概率密度函数(PDF):
对于连续随机变量,概率密度函数(PDF)描述了随机变量取某个值的概率密度。它用于定义在给定值附近的概率分布。对于一个随机变量X,其概率密度函数可表示为f(x)。对于任意给定的x,f(x)表示在x附近取值的概率密度。
累积分布函数(CDF):
累积分布函数(CDF)给出了随机变量小于或等于某个特定值的概率。对于一个随机变量X,其累积分布函数可表示为F(x)。给定一个特定的x,F(x)表示随机变量X小于或等于x的概率。
下面是使用Python代码绘制概率密度函数和累积分布函数的示例:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 创建一个正态分布随机变量
mu = 0 # 均值
sigma = 1 # 标准差
rv = norm(loc=mu, scale=sigma)
# 绘制概率密度函数(PDF)
x = np.linspace(-5, 5, 100) # x轴范围
pdf = rv.pdf(x) # 计算概率密度函数的值
plt.plot(x, pdf, label='PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('Probability Density Function (PDF)')
plt.legend()
# 绘制累积分布函数(CDF)
cdf = rv.cdf(x) # 计算累积分布函数的值
plt.figure()
plt.plot(x, cdf, label='CDF')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.title('Cumulative Distribution Function (CDF)')
plt.legend()
# 显示图形
plt.show()
代码中使用了SciPy库中的norm函数来创建一个均值为0、标准差为1的正态分布随机变量。然后利用pdf方法计算概率密度函数的值,并使用plot函数绘制PDF曲线。接着,利用cdf方法计算累积分布函数的值,并使用plot函数绘制CDF曲线。
执行上述代码后,将会显示出概率密度函数和累积分布函数的图像。这些图形可以帮助理解概率分布的特征,如密度的集中程度、分布的偏斜性以及随机变量小于或等于某个特定值的概率。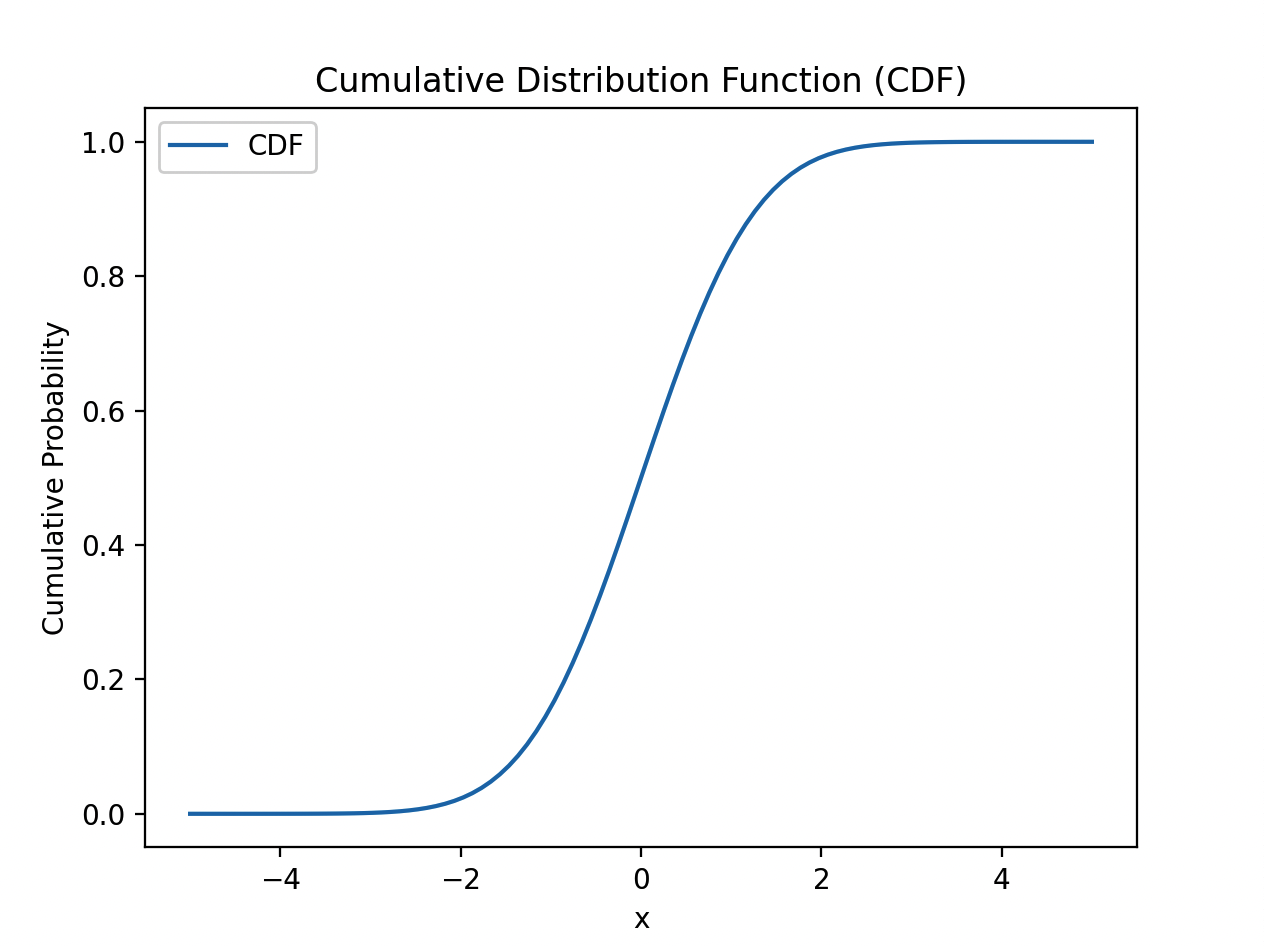

4、描述均值(平均值)、中位数和众数之间的区别,以及它们在统计中的应用。
均值(平均值)、中位数和众数是统计学中常用的描述数据集中趋势的指标,它们有不同的计算方法和应用场景。
- 均值(平均值)是一组数据的总和除以数据的个数。均值可以反映数据集的平均水平。在计算均值时,每个数据点都被等同对待,无论其大小或重要性。均值对极端值较为敏感,因为它会受到所有数据点的影响。
-
中位数是按照数值大小将一组数据划分为两个相等部分的值。中位数可被视为排序后的中间值,既不受极端值的影响,也不受数据分布的形态影响。中位数适用于处理存在异常值或偏斜分布的数据集。
-
众数是一组数据中出现次数最多的值。众数对离散数据具有描述性,可以确定数据集中最常见的值或模式。一个数据集可以有一个或多个众数,甚至可能没有众数。
在统计中的应用:
- 均值经常用作描述数据集整体趋势的指标,尤其适用于对称的数据分布。例如,在分析股票市场表现时,均值可以用来计算股票的平均收盘价。
-
中位数常用于处理有离群值的数据集。例如,当研究收入分布时,中位数可以更好地反映普通人的收入水平,而不受富豪或贫困人群的影响。
-
众数常用于描述离散型数据的最常见取值或模式。例如,研究一个班级学生的血型分布时,可能会找到最常见的血型并报告其为众数。
一个例子
假设我们有一组考试成绩数据:65, 72, 81, 88, 90。
- 均值:(65 + 72 + 81 + 88 + 90) / 5 = 79.2。均值表示这些成绩的平均水平。
-
中位数:对数据进行排序后,中间值为81。中位数表示在一半学生的成绩高于81,另一半低于81。
-
众数:没有重复的值,所以没有众数。
在此案例中,均值和中位数都提供了数据集的集中趋势信息。均值是较大值和较小值的平均值,而中位数则是排序后的中间值。它们可以帮助我们理解整体成绩水平和分布的中心位置。
5、什么是方差和标准差?它们如何衡量数据的分散程度?
方差(variance)和标准差(standard deviation)是两种常用的统计量,用于衡量数据的分散程度。
方差是指数据点与其均值之间的偏离程度的平均值。它通过计算每个数据点与均值的差值的平方,然后取平均得到。方差的公式如下:
$$
\text{方差} = \frac{\sum_{i=1}^{n}(x_i – \bar{x})^2}{n}
$$
其中,$x_i$ 是第 $i$ 个数据点,$\bar{x}$ 是所有数据点的均值,$n$ 是数据点的总数。
标准差是方差的平方根,它表示数据点与均值之间的差异程度。标准差通常用于评估数据的离散程度,数值越大表示数据越分散,数值越小表示数据越接近均值。标准差的公式如下:
$$
\text{标准差} = \sqrt{\text{方差}}
$$
下面通过一个具体案例来说明方差和标准差的计算过程。
假设我们有一组数据:2, 4, 6, 8, 10。首先计算均值:
$$
\bar{x} = \frac{2 + 4 + 6 + 8 + 10}{5} = 6
$$
然后计算方差,即每个数据点与均值之差的平方的平均:
$$
\text{方差} = \frac{(2-6)^2 + (4-6)^2 + (6-6)^2 + (8-6)^2 + (10-6)^2}{5} = 8
$$
最后计算标准差,即方差的平方根:
$$
\text{标准差} = \sqrt{8} \approx 2.83
$$
因此,这组数据的方差为8,标准差为2.83。方差和标准差的数值表示数据的分散程度,较大的数值意味着数据点相对于均值的离散程度更高。
6、什么是正态分布(Normal Distribution)?它的特点是什么,以及在实际应用中的重要性是什么?
正态分布(Normal Distribution),也称为高斯分布(Gaussian Distribution),是统计学中最常见的连续概率分布之一。它在自然界和许多实际应用中都具有重要性。
正态分布的特点如下:
- 对称性:正态分布呈现对称的钟形曲线,均值位于分布的中心,两侧的尾部逐渐趋近于零。
-
唯一标识:正态分布由两个参数完全确定,即均值(μ)和标准差(σ),其中均值决定了分布的位置,标准差决定了分布的形状。
-
中心极限定理:正态分布是许多随机现象的结果,根据中心极限定理,当独立随机变量求和时,其总和的分布趋向于正态分布。
-
68-95-99.7规则:约有68%的数据落在均值的一个标准差范围内,约有95%的数据落在均值的两个标准差范围内,约有99.7%的数据落在均值的三个标准差范围内。
正态分布在实际应用中具有重要性的原因如下:
- 数据建模:许多实际观测的数据可以近似地服从正态分布。因此,正态分布可用于对这些数据进行建模和分析。
-
统计推断:许多经典的统计推断方法,如假设检验和置信区间估计,基于正态分布的性质进行计算。
-
预测和控制:正态分布在预测和控制问题中起着重要作用。例如,在质量控制中,正态分布被用来设置规范限和判断过程是否稳定。
-
自然现象:许多自然现象和人类行为都可以用正态分布来描述,如身高、体重、IQ分数等。
正态分布的重要性在于其具有广泛的适用性和数学性质的良好性质。它在统计学和各个领域的科学研究中扮演着重要角色,并且为我们提供了一种常见的模型来理解数据分布和进行概率推断。
以下是一个实际开源的正态分布案例,使用了来自Kaggle网站的”House Prices: Advanced Regression Techniques”数据集中的房屋销售价格数据。
[208500, 181500, 223500, 140000, 250000, 143000, 307000, 200000, 129900, 118000, 129500, 345000, 144000, 279500, 157000, 132000, 149000, 90000, 159000, 139000]
这些数据代表不同房屋的销售价格(以美元为单位)。我们可以对这些数据进行统计分析,计算均值和标准差,并通过绘制直方图或概率密度函数图形来探索它们是否近似于正态分布。
可以使用Python的数据分析库(例如matplotlib和numpy)来绘制给定数据的直方图。以下是使用Python生成直方图的示例代码:
import matplotlib.pyplot as plt
import numpy as np
data = [208500, 181500, 223500, 140000, 250000, 143000, 307000, 200000, 129900, 118000, 129500, 345000, 144000, 279500, 157000, 132000, 149000, 90000, 159000, 139000]
# Set the bins and number of intervals for the histogram
bin_edges = np.linspace(min(data), max(data), num=10)
# Plot the histogram
plt.hist(data, bins=bin_edges, edgecolor='black')
# Add labels and title
plt.xlabel('House Sale Prices')
plt.ylabel('Frequency')
plt.title('Distribution of House Sale Prices')
# Show the plot
plt.show()
运行此代码将生成一个直方图,显示了房屋销售价格的分布情况。横轴表示价格区间,纵轴表示频数或计数。
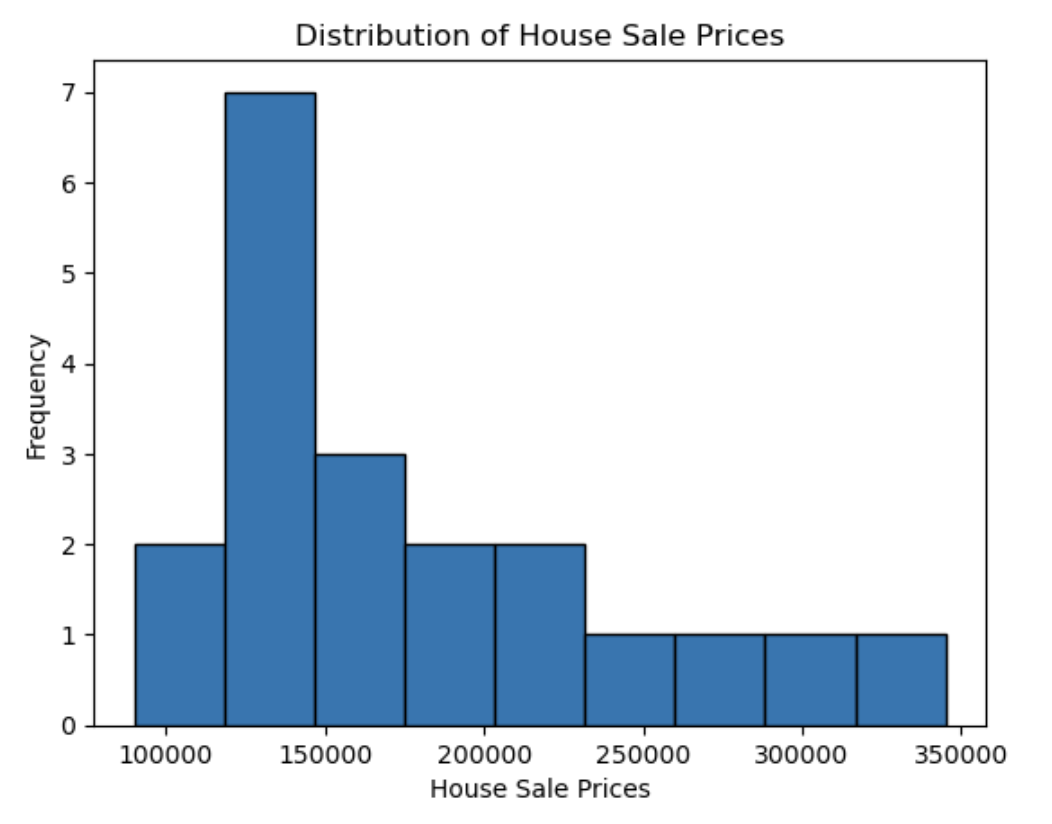
7、假设检验的概念,以及在统计学中如何使用它来验证假设。
假设检验是统计学中的一种方法,用于验证关于总体参数或数据集特征的假设。它提供了一种科学的方式来判断样本数据是否支持或反驳某个假设。
在使用假设检验时,通常有两个假设:零假设(null hypothesis)和备择假设(alternative hypothesis)。零假设表示我们要进行检验的假设,而备择假设则是对零假设的对立或替代假设。
假设检验的步骤如下:
- 建立假设:明确零假设和备择假设。
-
选择显著性水平:确定接受或拒绝零假设的临界值。
-
收集数据:收集与问题相关的数据。
-
计算统计量:根据数据计算出适当的统计量。
-
计算P值:根据统计量计算出P值,即给定观察到的数据情况下,零假设成立的概率。
-
做出决策:将P值与显著性水平进行比较,并基于P值做出接受或拒绝零假设的决策。
-
得出结论:根据决策结果得出关于零假设的结论。
一个实际的案例是检验一种新药物是否有效。假设我们想要测试新药物对某种疾病的疗效,零假设为”新药物无效”,备择假设为”新药物有效”。我们进行了一项随机对照试验,将患者分为两组,其中一组接受新药物治疗,另一组接受安慰剂。
收集得到的数据如下:
- 新药物组平均疗效:82%
-
安慰剂组平均疗效:75%
现在我们需要使用假设检验来验证该新药物是否有效。我们可以采用配对样本t检验,计算出适当的统计量,并计算P值。根据P值与预先确定的显著性水平进行比较,如果P值小于显著性水平(通常为0.05),则我们可以拒绝零假设,得出结论认为新药物是有效的。否则,我们无法拒绝零假设,即没有足够的证据支持新药物的疗效。
请注意,实际的假设检验涉及更复杂的统计方法和假设情景,但这个案例提供了一个简化的示例来说明假设检验的概念和使用方法。
8、什么是统计抽样和抽样分布?中心极限定理(Central Limit Theorem)对统计有什么重要影响?
统计抽样是指从一个总体中选择一部分个体作为样本的过程。通过对样本进行研究和分析,我们可以推断出有关总体的特征、参数或关系的信息。
抽样分布是指在重复从总体中抽取样本,并计算某个统计量(例如均值、比例等)的情况下,该统计量的分布。抽样分布可以帮助我们了解样本统计量的变异性以及与总体参数之间的关系。
中心极限定理(Central Limit Theorem, CLT)是统计学中的一个重要理论。它指出,当从任何总体中抽取足够大的样本时,样本平均值的分布会近似于正态分布,无论总体分布形态如何。
具体而言,中心极限定理包含以下关键观点:
- 抽样分布的均值接近于总体均值。
-
抽样分布的标准差接近于总体标准差除以样本大小的平方根。
-
抽样分布呈现出对称的钟形曲线。
中心极限定理对统计学有着重要的影响,因为它使得我们能够在不知道总体分布的情况下进行推断和假设检验。通过从总体中抽取样本,无论总体分布如何,我们可以利用抽样分布近似于正态分布的特点,应用基于正态分布的统计方法来做出推断。这使得统计学成为了现代科学、工程和社会科学中不可或缺的一部分。
9、置信区间(Confidence Interval)和假设检验中的p值(p-value)的含义和用途。
置信区间(Confidence Interval)是一个用于估计总体参数的范围。它提供了一个区间,我们可以合理地认为总体参数在该区间内。置信区间通常以特定的置信水平表示,例如95%或99%。具体而言:
- 在给定的置信水平下,置信区间是样本统计量的上下界限,使得在重复抽样中有一定比例的区间包含真实的总体参数值。
-
如果我们使用不同的样本进行重复实验,并计算出置信区间,有限个实验中有约95%的置信区间将包含总体参数。
p值(p-value)是假设检验中的一个度量,表示观察到的数据或更极端情况出现的概率,假设零假设为真。具体而言:
- p值表示在零假设成立的条件下,观察到的样本结果或更极端结果出现的概率。
-
通过与预先选定的显著性水平进行比较,可以根据p值来判断是否拒绝零假设。
-
如果p值小于显著性水平(通常为0.05),则我们有足够的证据拒绝零假设;否则,我们无法拒绝零假设。
在统计推断中,置信区间和p值都用于对总体参数进行推断和假设检验:
- 置信区间提供了一个区间范围,我们可以合理地认为总体参数在其中。它用于估计总体参数的不确定性,并给出一个范围的估计。
-
p值则用于评估样本数据与零假设一致的程度。它提供了一个基于观察数据的量化指标,以帮助我们决定是否拒绝或接受零假设。
这两个概念在统计学中是常用的工具,用于推断总体参数、比较组之间的差异,并从数据中得出可靠的结论。
