三、决策树

决策树

1、什么是决策树，它是如何工作的？简要描述其基本原理。

决策树（Decision Tree）是一种用于分类和回归问题的机器学习模型。它是一个树状结构，其中每个节点代表一个特征，每个分支代表一个特征值，每个叶子节点代表一个类别或回归值。

决策树的基本原理是根据输入特征逐步分割数据集，以便最终能够根据特征的值来预测目标变量的类别或值。

基本工作原理：

1、根节点：开始时，整个数据集视为一个根节点。在根节点上，选择一个特征，将数据集分割成多个子集。选择的特征是基于某种度量标准，通常是根据信息增益（Entropy）、基尼不纯度（Gini Impurity）或均方误差（Mean Squared Error）等来进行选择。

2、分支节点：接下来，每个子集都被视为一个分支节点，并在分支节点上选择另一个特征，再次将数据集分割成更小的子集。这个过程递归地进行下去，直到达到某个停止条件，如达到最大深度、节点中的样本数小于阈值，或者节点的不纯度低于阈值。

3、叶子节点：当不再进行分割时，节点被标记为叶子节点，叶子节点中包含一个最终的类别标签（对于分类问题）或回归值（对于回归问题）。这个值是根据该节点上的数据集的主要类别（对于分类问题）或平均目标值（对于回归问题）来确定的。

4、预测：一旦构建了决策树，对新的未见样本进行预测时，从根节点开始根据特征的值遍历树的分支，直到达到叶子节点。然后，将叶子节点的类别标签或回归值作为预测结果。

决策树的优点包括易于理解和解释，能够处理数值和分类特征，对异常值不敏感。

然而，它也容易过拟合，因此需要进行剪枝等正则化操作以提高泛化能力。

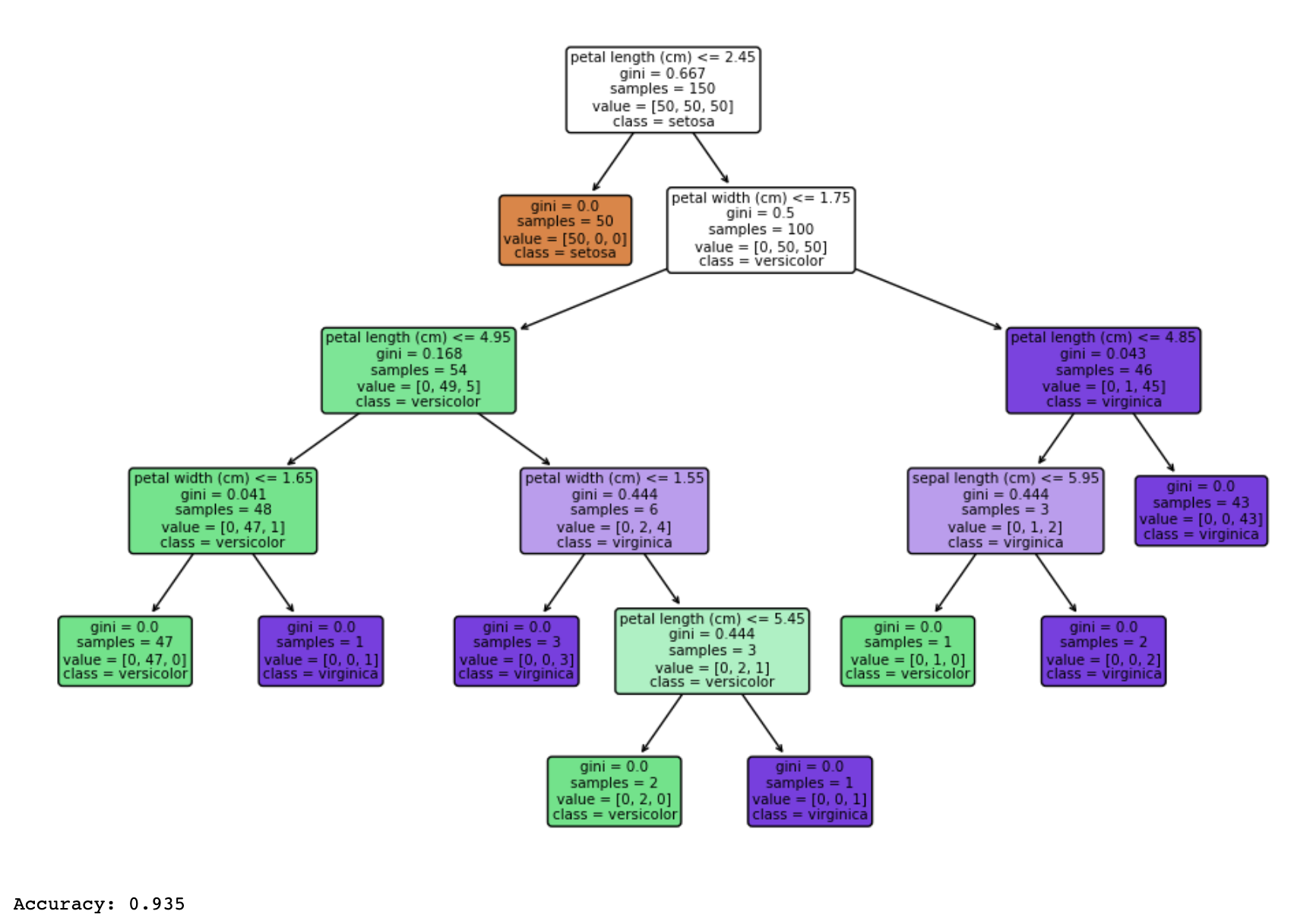
下面使用Python的Scikit-Learn库的简单决策树分类的示例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier 
from sklearn import tree

# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 创建并拟合决策树分类器
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X, y)

# 将类别名称转换为列表
class_names = iris.target_names.tolist()

# 可视化决策树
plt.figure(figsize=(12, 8))
tree.plot_tree(clf, 
               feature_names=iris.feature_names, 
               class_names=class_names,  # 使用Python列表而不是NumPy数组
               filled=True, 
               rounded=True)
plt.show()

accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

上述代码示例使用鸢尾花数据集，构建了一个决策树分类器，对花的种类进行分类。然后，使用测试集对模型进行评估，计算了准确度作为性能指标。

2、决策树的构建过程中有哪些常用的划分准则（splitting criterion）？如何选择最佳划分准则？

决策树的构建过程中常用的划分准则有三种：

• 信息增益（Information Gain）
• 基尼不纯度（Gini Impurity）
• 均方误差（Mean Squared Error）

这些准则用于确定在每个节点上如何划分数据，以选择最佳的特征和划分方式。

划分准则的解释：

1、信息增益（Information Gain）：信息增益是用于分类问题的常见划分准则，它基于信息论的概念。在每个节点上，根据特征的取值将数据集分成多个子集，然后计算每个子集的熵（Entropy），然后计算信息增益，它是父节点熵与子节点熵之差。信息增益越大，意味着划分后的数据更加纯净，更有助于分类。

选择信息增益最大的特征作为划分特征，可以使用熵的减少量来衡量。信息增益的问题是它偏向于选择具有较多取值的特征。

2、基尼不纯度（Gini Impurity）：基尼不纯度是另一种用于分类问题的划分准则。在每个节点上，根据特征的取值将数据集分成多个子集，然后计算每个子集的基尼不纯度，它表示从该子集中随机选择两个样本，它们的类别标签不一致的概率。基尼不纯度越低，表示子节点的纯度越高。

选择基尼不纯度最低的特征作为划分特征。基尼不纯度相对于信息增益更加偏好选择取值较少的特征，因此在某些情况下，它可能会对多分类问题更有利。

3、均方误差（Mean Squared Error）：均方误差是用于回归问题的划分准则。在每个节点上，根据特征的取值将数据集分成多个子集，然后计算每个子集中目标变量的均方误差。均方误差越低，表示子节点的目标变量值更接近于均值，模型对数据的拟合越好。

选择均方误差最低的特征作为划分特征。均方误差通常用于回归决策树。

选择最佳划分准则的方法通常取决于问题的性质和数据集的特点。在Scikit-Learn等机器学习库中，可以使用参数来指定划分准则。通常，信息增益和基尼不纯度用于分类问题，而均方误差用于回归问题。为了选择最佳特征和划分，决策树算法会尝试所有可能的特征和取值组合，并选择最优的划分方式，这个过程通常称为”贪心”方法。

需要注意的是，在决策树构建过程中，还可以应用剪枝（pruning）等技术来避免过拟合，提高模型的泛化性能。选择合适的划分准则和适当的剪枝策略对于构建高性能的决策树模型非常重要。

3、什么是过拟合（overfitting）？在决策树中如何避免过拟合？

过拟合（Overfitting）是指机器学习模型在训练数据上表现很好，但在未见过的测试数据上表现较差的现象。它表示模型过度适应了训练数据的噪声和细节，导致模型在面对新数据时泛化能力差。过拟合通常表现为模型在训练数据上的误差非常低，但在测试数据上的误差却较高。

在决策树中避免过拟合的方法：

1、剪枝（Pruning）：剪枝是一种减小树的复杂度的方法，它通过移除一些叶子节点或将一些子树替换为叶子节点来降低模型的复杂度。这有助于减少模型对训练数据的拟合程度，提高模型的泛化能力。剪枝的关键是确定何时停止分裂节点以及如何选择要剪枝的节点。常用的剪枝策略包括预剪枝和后剪枝。

2、限制树的深度（Max Depth）：限制树的深度是一种简单而有效的方法，通过设置树的最大深度可以控制树的复杂度。树的深度过大会增加过拟合的风险，因此限制树的深度有助于提高模型的泛化性能。

3、增加最小样本数（Min Samples）：通过设置每个叶子节点的最小样本数，可以控制叶子节点的数量。增加最小样本数可以防止生成过于细分的叶子节点，从而减少模型的过拟合风险。

4、限制叶子节点的最小样本数（Min Samples per Leaf）：与上一点类似，但是是限制每个叶子节点的最小样本数。这有助于确保叶子节点中的样本数量不会太少，从而减少过拟合。

5、降低信息增益（Information Gain）阈值：信息增益用于选择划分特征，降低信息增益的阈值可以使模型更加保守，减少过度划分的可能性。

6、随机森林（Random Forest）：随机森林是一种基于决策树的集成方法，通过随机选择特征子集和样本子集来构建多棵树，并将它们组合起来进行预测。随机森林通常能够降低过拟合风险，提高模型的泛化性能。

避免过拟合是决策树模型中的一个关键问题，需要根据具体问题和数据集选择适当的方法来控制模型的复杂度。通常，通过组合多种策略，可以有效地减轻过拟合问题，使决策树模型更加稳健。

4、决策树的剪枝是什么？它的作用是什么，如何执行剪枝操作？

决策树的剪枝是一种用于减小树的复杂度、防止过拟合的技术。它的主要作用是通过修剪决策树的一部分（通常是叶子节点）来降低模型的复杂度，从而提高模型的泛化能力。剪枝是为了在保持模型预测能力的同时，减少模型对训练数据中噪声和细节的过度拟合。

剪枝的基本思想是删除一些子树，使树变得更简单。在剪枝过程中，一些叶子节点可能会被合并，或者一些分支可能会被删除，以减少树的深度和复杂度。剪枝的目标是找到一个合适的平衡点，即在保持模型性能的前提下，降低树的复杂度。

剪枝操作的一般步骤：

1、自底向上选择节点：剪枝通常从叶子节点开始，逐渐向上选择节点进行剪枝。这是因为剪枝操作从叶子节点开始，不会影响上层节点的判断，因此更容易控制模型的复杂度。

2、计算剪枝前后的性能：对每个选择的节点，计算剪枝前后模型在验证集或测试集上的性能。通常使用交叉验证或留出法来评估模型性能。

3、进行剪枝：根据性能评估，决定是否进行剪枝。如果剪枝后模型性能没有显著下降，可以执行剪枝操作。剪枝的具体方式包括删除子树、将节点变为叶子节点、合并相邻的叶子节点等。

4、递归操作：一旦剪枝完成，需要递归地向上处理父节点，检查是否需要剪枝。这个过程一直持续到根节点。

剪枝操作通常需要根据数据和具体问题来调整，因为过度剪枝会导致欠拟合，而不足剪枝会导致过拟合。为了确定合适的剪枝策略，可以使用交叉验证来评估不同剪枝参数的性能，选择在验证集上性能最佳的模型。 Scikit-Learn等机器学习库通常提供了自动剪枝功能，你可以通过设置相关参数来控制剪枝过程。

5、熵（entropy）和信息增益（information gain）在决策树中的角色。它们如何帮助选择最佳特征进行划分？

熵 和 信息增益 是在决策树中用于特征选择的重要概念，它们帮助选择最佳特征进行划分。

1、熵（Entropy）：熵是信息论中用来度量不确定性或混乱程度的概念。在决策树中，熵被用来度量一个节点的不纯度，即该节点包含多少不同类别的样本。

熵的计算公式：

对于节点 $t$，$p_i$ 表示类别 $i$ 在节点 $t$ 中的样本比例。

$$
\text{Entropy}(t) = -\sum_{i=1}^{c} p_i \log_2(p_i)
$$
其中，$c$ 表示类别的数量。熵的值在0和1之间，越接近0表示节点越纯净，越接近1表示节点的不纯度越高。

2、信息增益（Information Gain）：信息增益用于选择最佳特征来划分数据集。它衡量了通过选择某个特征进行划分后，父节点的熵减少了多少，即子节点的不纯度相对于父节点而言减少了多少。

信息增益的计算公式：
$$
\text{Information Gain}(D, A) = \text{Entropy}(D) – \sum_{v \in \text{Values}(A)} \frac{|D_v|}{|D|} \text{Entropy}(D_v)
$$
其中，$D$ 是父节点的数据集，$A$ 是要划分的特征，$\text{Values}(A)$ 是特征 $A$ 的取值集合，$D_v$ 是特征 $A$ 取值为 $v$ 时的子节点数据集。

信息增益的目标是选择使得信息增益最大的特征来进行划分，因为最大的信息增益意味着划分后的子节点更纯净，不确定性更低。因此，信息增益可以帮助决策树选择最能有效地划分数据的特征，从而构建更加有用的决策树模型。

需要注意的是，信息增益在选择特征时有一定的偏向性，它倾向于选择取值较多的特征，因此在某些情况下可能不适用。为了解决这个问题，基尼不纯度（Gini Impurity）是另一种可选的划分准则，它在某些情况下更适用于特征选择。在实际应用中，可以根据具体问题和数据集选择适当的划分准则。

6、什么是基尼不纯度（Gini impurity）？它与信息增益有何不同？在什么情况下应该使用基尼不纯度？

基尼不纯度是一种用于决策树中的划分准则，它用来度量一个节点的不纯度或混乱程度。

基尼不纯度越低，表示节点的纯度越高，即该节点包含的样本更倾向于属于同一类别。与信息增益不同，基尼不纯度不依赖于对数，计算相对较为简单。

基尼不纯度的计算公式：

对于节点 $t$，$p_i$ 表示类别 $i$ 在节点 $t$ 中的样本比例。

$$
\text{Gini}(t) = 1 – \sum_{i=1}^{c} (p_i)^2
$$
其中，$c$ 表示类别的数量。基尼不纯度的值在0和1之间，越接近0表示节点越纯净，越接近1表示节点的不纯度越高。

与信息增益相比，基尼不纯度有一些不同之处：

1、计算方式：信息增益使用对数计算，而基尼不纯度使用平方计算。这意味着基尼不纯度对误分类的惩罚相对较小，因此更偏向于选择具有最大基尼不纯度下降的特征。

2、取值范围：信息增益的取值范围在0到1之间，而基尼不纯度的取值范围也在0到1之间，但通常基尼不纯度的值略高于信息增益。

3、应用场景：基尼不纯度在某些情况下更适用于特征选择。特别是在处理多分类问题（类别数较多）时，基尼不纯度通常表现更好，因为它偏向于选择取值较少的特征，可以降低树的复杂度。

在选择划分特征时，可以根据具体问题和数据集的特点选择使用信息增益或基尼不纯度。通常情况下，它们都是有效的划分准则，但在不同情况下可能表现出不同的优势。机器学习库（如Scikit-Learn）通常提供了两者的选项，以便根据问题需求进行选择。

7、决策树可以用于分类和回归问题，它们的主要区别是什么？如何将决策树应用于回归问题？

决策树是一种用于分类和回归问题的机器学习模型，它们的主要区别在于应用的问题类型和输出变量的性质。

分类问题：

• 在分类问题中，目标是将输入数据分为预定义的类别或标签中的一个。决策树用于解决分类问题时，每个叶子节点代表一个类别，模型通过从根节点到叶子节点的路径来确定数据点的类别。例如，可以使用决策树来判断电子邮件是垃圾邮件还是正常邮件、患者是否患有某种疾病等。

回归问题：

• 在回归问题中，目标是预测一个连续的数值输出，而不是分类标签。决策树用于解决回归问题时，每个叶子节点代表一个数值，模型通过从根节点到叶子节点的路径来预测数据点的数值输出。例如，可以使用决策树来预测房屋价格、股票价格等连续性输出。

主要区别：

• 主要区别在于输出变量的性质。分类问题的输出是离散的类别标签，而回归问题的输出是连续的数值。决策树的构建和评估方法在两种问题中基本相同，但叶子节点的表示和预测方式不同。

将决策树应用于回归问题

要将决策树应用于回归问题，需要对其进行一些适应性修改。

以下是一些将决策树用于回归问题的关键点：

1、叶子节点的表示：在回归决策树中，叶子节点不再代表类别标签，而代表数值。通常，叶子节点的数值是该节点中所有训练样本的目标变量值的平均值。

2、划分准则：在回归决策树中，常用的划分准则包括均方误差（Mean Squared Error）和平均绝对误差（Mean Absolute Error）。划分时选择使均方误差或平均绝对误差最小化的特征和取值。

3、剪枝：与分类决策树类似，回归决策树也可以进行剪枝操作，以减小树的复杂度，提高泛化能力。

4、评估指标：在回归问题中，通常使用均方误差、平均绝对误差、决定系数（R-squared）等指标来评估模型的性能。

使用Scikit-Learn中的决策树模型解决回归问题：

from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 载入波士顿房价数据集
data = load_boston()
X = data.data
y = data.target

# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 建立回归决策树模型
regressor = DecisionTreeRegressor()

# 模型训练
regressor.fit(X_train, y_train)

# 模型预测
y_pred = regressor.predict(X_test)

# 评估模型性能
mse = mean_squared_error(y_test, y_pred)
print("Mean Squared Error:", mse)

上述代码示例使用波士顿房价数据集，构建了一个回归决策树模型，并使用均方误差（Mean Squared Error）来评估模型的性能。

8、随机森林是什么，它是如何改进单个决策树模型的性能的？

随机森林（Random Forest）是一种集成学习算法，用于改进单个决策树模型的性能。是一种强大且广泛应用的机器学习方法。

随机森林的核心思想是通过构建多个决策树，并将它们的预测结果结合起来，来提高整体模型的性能和鲁棒性。

以下是随机森林是如何改进单个决策树模型性能的主要方式：

1、随机抽样（Bootstrap抽样）：在构建每棵决策树时，随机森林从训练数据中使用有放回抽样（Bootstrap抽样）来创建不同的训练子集。这意味着每棵树使用的数据集都是略有不同的，从而增加了模型的多样性。

2、随机特征选择：在每次分裂决策树节点时，随机森林不考虑所有特征，而是从所有特征中随机选择一个子集用于分裂。这样可以防止某些特征在模型中占据主导地位，增加了模型的多样性，同时也提高了计算效率。

3、多数投票或平均：当随机森林中的所有决策树都构建完成后，它们的预测结果会被结合起来。对于分类问题，采用多数投票的方式，即每棵树投票选择类别，最终选择得票最多的类别作为模型的预测结果。对于回归问题，采用平均的方式，即将所有树的预测结果取平均值作为最终预测值。

4、降低过拟合风险：由于随机森林的每个决策树都是在不同的子集上训练的，因此它们具有较高的多样性，降低了过拟合的风险。这意味着即使训练数据中存在噪声或异常值，随机森林也能够产生稳健的预测。

5、高性能：随机森林通常在处理大规模数据集时表现良好，因为每棵决策树可以并行构建，从而提高了训练速度。此外，它们通常不需要太多的超参数调整，使其易于使用。

总的来说，随机森林通过组合多个决策树，利用随机性和投票策略，改进了单个决策树的性能，提高了模型的泛化能力和鲁棒性，适用于各种机器学习任务，包括分类、回归和特征选择。