通透！归一化总结！！

统一尺度：当数据集中的特征在不同的尺度上时（例如，一个特征的范围是0到1，另一个是100到1000），归一化可以将所有特征转换到相似的尺度上。
提高收敛速度：在使用梯度下降和其他基于优化的算法时，归一化可以帮助加快收敛速度。如果特征在不同尺度上，优化过程可能会变得非常慢。
防止偏差：在一些算法中，例如距离计算的算法（如K-最近邻、K-均值聚类），如果一个特征的数值范围比其他特征大得多，那么它可能会在距离计算中起主导作用，从而影响算法的性能。
提高数值稳定性：归一化还可以避免数值计算中的问题，如梯度消失或爆炸，这在深度学习模型中尤其重要。

聊完归一化的几个关键点，再来详细阐述一下，开头说的重要性，重要在哪几方面：

加速模型训练：归一化后的数据有助于加速学习算法的收敛。在很多算法（如梯度下降）中，如果特征具有不同的尺度，会导致收敛缓慢或不稳定。
提高模型性能：当特征在相似的尺度上时，模型训练更加高效，可以提高模型的性能。不同尺度的特征可能会导致模型偏向于尺度较大的特征。
降低数值计算难度：归一化可以减少数值计算的复杂性，尤其是对于基于距离的算法（如K-最近邻或K-均值聚类），不同尺度的特征可能会对距离计算产生不均等的影响。
避免数值不稳定性和提高精度：在许多机器学习算法中，非常高或非常低的值可能导致数值不稳定，如梯度爆炸或消失。归一化有助于避免这些问题。
使特征更加统一：在涉及多个特征的数据集中，归一化确保每个特征被赋予等同的重要性。没有归一化，具有较大范围的特征可能会不成比例地影响结果。
更好地理解特征重要性：在归一化后，特征的权重大小可以直接表明其对模型的影响，从而更容易解释模型。
适应特定算法要求：某些机器学习算法，尤其是基于梯度的优化算法和正则化方法，要求数据必须归一化才能正确工作。

说了这么多，从概念上，我想大家已经大概对于归一化有了一个宏观的认识。

下面咱们从代码层面，说说几种不同的归一化方法，以及归一化带来的效果。

最小-最大归一化
标准化
小数定标归一化
均值归一化
单位长度归一化

咱们一起来看看~

最小-最大归一化

最小-最大归一化是一种将数据特征缩放到特定范围（通常是0到1）的方法。该方法对原始数据进行线性变换，确保数据的最小值变为0，最大值变为1。这种归一化方法对原始数据的分布形状没有影响，仅改变数据的尺度和位置。

公式说明

设 $ X $ 为原始数据集，$ x $ 为 $ X $ 中的任意数据点。最小-最大归一化的公式为：

$$
x_{\text{norm}} = \frac{x – \min(X)}{\max(X) – \min(X)}
$$
其中，$ \min(X) $ 和 $ \max(X) $ 分别是数据集 $ X $ 中的最小值和最大值。经过这个公式处理后，$ x_{\text{norm}} $ 的值将位于0和1之间。

计算步骤

确定数据集 $ X $ 中的最小值 $ min(X) $ 和最大值 $ max(X) $。
对于数据集 $ X $ 中的每个数据点 $ x $，使用上述公式计算 $ x_{text{norm}} $。

案例代码

以下代码包括数据生成、归一化处理，以及可视化对比结果。

import numpy as np
import matplotlib.pyplot as plt

# 生成两组不同尺度的数据
data_small_scale = np.random.randint(0, 100, 100)  # 范围在0到100
data_large_scale = np.random.randint(1000, 10000, 100)  # 范围在1000到10000

# 最小-最大归一化
def min_max_normalize(data):
    return (data - np.min(data)) / (np.max(data) - np.min(data))

# 应用最小-最大归一化
normalized_small_scale = min_max_normalize(data_small_scale)
normalized_large_scale = min_max_normalize(data_large_scale)

# 可视化对比
plt.figure(figsize=(12, 6))

# 绘制原始数据的直方图
plt.subplot(221)
plt.hist(data_small_scale, bins=15, color='blue', alpha=0.7)
plt.title('Small Scale Data')
plt.xlabel('Value')
plt.ylabel('Frequency')

plt.subplot(222)
plt.hist(data_large_scale, bins=15, color='red', alpha=0.7)
plt.title('Large Scale Data')
plt.xlabel('Value')
plt.ylabel('Frequency')

# 绘制归一化数据的直方图
plt.subplot(223)
plt.hist(normalized_small_scale, bins=15, color='green', alpha=0.7)
plt.title('Normalized Small Scale Data')
plt.xlabel('Normalized Value')
plt.ylabel('Frequency')

plt.subplot(224)
plt.hist(normalized_large_scale, bins=15, color='orange', alpha=0.7)
plt.title('Normalized Large Scale Data')
plt.xlabel('Normalized Value')
plt.ylabel('Frequency')

plt.tight_layout()
plt.show()

在这段代码中，定义了一个 min_max_normalize 函数来应用最小-最大归一化。

归一化前后对比

要清楚地展示归一化前后数据的差异，我们可以采取以下两种方法：

不同尺度的特征组合：我们可以创建两组特征，其中一组的尺度远大于另一组，然后展示归一化对这些特征的影响。这种情况更贴近现实世界的数据，其中不同特征可能有非常不同的尺度。
直观的坐标轴比较：我们可以在同一图中绘制原始数据和归一化后的数据，但使用不同的坐标轴，以便直观地比较两者的尺度差异。

我将按照第一种方法进行操作，生成两组数据：一组范围在0到100，另一组范围在1000到10000。然后，我们将应用最小-最大归一化并比较结果。

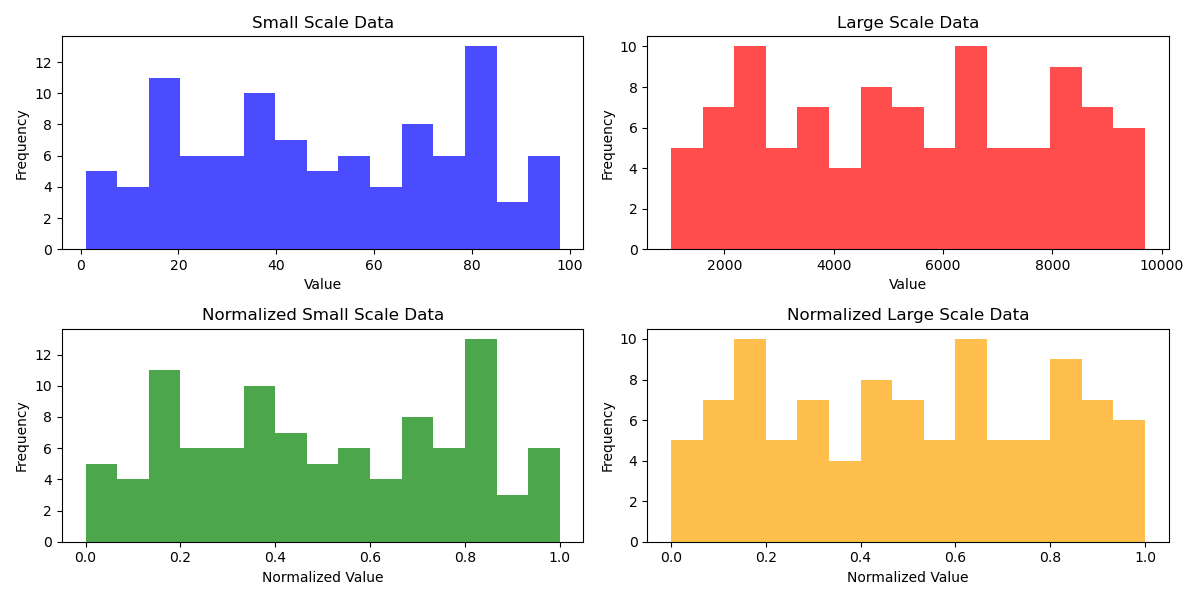
在这个图中，我们展示了两组不同尺度的数据及其归一化后的结果。

左上图：显示了小尺度数据（0到100）的分布。
右上图：展示了大尺度数据（1000到10000）的分布。

这两组数据在尺度上有显著差异，这在现实世界的数据集中是常见的情况。接下来，我们看到归一化后的结果：

左下图：小尺度数据经过归一化后的分布，所有值都被缩放到了0到1之间。
右下图：大尺度数据经过归一化后的分布，同样被缩放到了0到1之间。

通过这种比较，可以清楚地看到归一化处理对于不同尺度数据的影响。无论原始数据的尺度多大，归一化都能将其有效地转换到相同的尺度上，这对于确保机器学习模型的性能和稳定性至关重要。特别是在涉及多个特征，且这些特征具有不同尺度的情况下，归一化可以帮助模型更有效地学习和理解数据。

下面几种归一化方法，咱们结合具体的算法模型来说说~

标准化

标准化（Standardization）将数据调整为具有均值为0和标准差为1的分布。这种处理对于许多机器学习算法是重要的，因为它们假设所有特征都是以同样的规模（比如，高斯分布）测量的。

公式推导

对于数据集 $X$ 中的每个特征 $x_i$，标准化可以表示为：
$$
z_i = \frac{x_i – \mu}{\sigma}
$$
其中，$\mu$ 是特征的平均值，$\sigma$ 是标准差。这个转换保证了特征 $z_i$ 的均值为0，标准差为1。

计算步骤

计算均值和标准差：对于数据集中的每个特征，计算其均值和标准差。
应用转换：使用上述公式将每个特征值转换为标准化值。

案例代码

这个例子中，我们使用支持向量机（SVM）作为算法模型，展示标准化对模型性能的影响。

使用Python的scikit-learn库来实现这一点，并使用make_classification来生成虚拟的分类数据集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score

# 生成虚拟数据集
X, y = make_classification(n_samples=1000, n_features=2, n_redundant=0, n_clusters_per_class=1, random_state=42)

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 未标准化的SVM模型
model = SVC(kernel='linear')
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy_non_standardized = accuracy_score(y_test, y_pred)

# 应用标准化
scaler = StandardScaler()
X_train_standardized = scaler.fit_transform(X_train)
X_test_standardized = scaler.transform(X_test)

# 标准化的SVM模型
model_standardized = SVC(kernel='linear')
model_standardized.fit(X_train_standardized, y_train)
y_pred_standardized = model_standardized.predict(X_test_standardized)
accuracy_standardized = accuracy_score(y_test, y_pred_standardized)

# 结果展示
print(f'Accuracy with non-standardized data: {accuracy_non_standardized}')
print(f'Accuracy with standardized data: {accuracy_standardized}')

# 可视化
plt.figure(figsize=(12, 5))

# 绘制未标准化数据
plt.subplot(1, 2, 1)
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train)
plt.title("Distribution of Non-Standardized Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

# 绘制标准化数据
plt.subplot(1, 2, 2)
plt.scatter(X_train_standardized[:, 0], X_train_standardized[:, 1], c=y_train)
plt.title("Distribution of Standardized Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

plt.show()

在这段代码中，我们首先生成一个虚拟的二维分类数据集。然后，我们训练了两个SVM模型，一个使用未标准化数据，另一个使用标准化数据。

通过比较这两个模型的准确率，我们可以看到标准化对模型性能的影响。

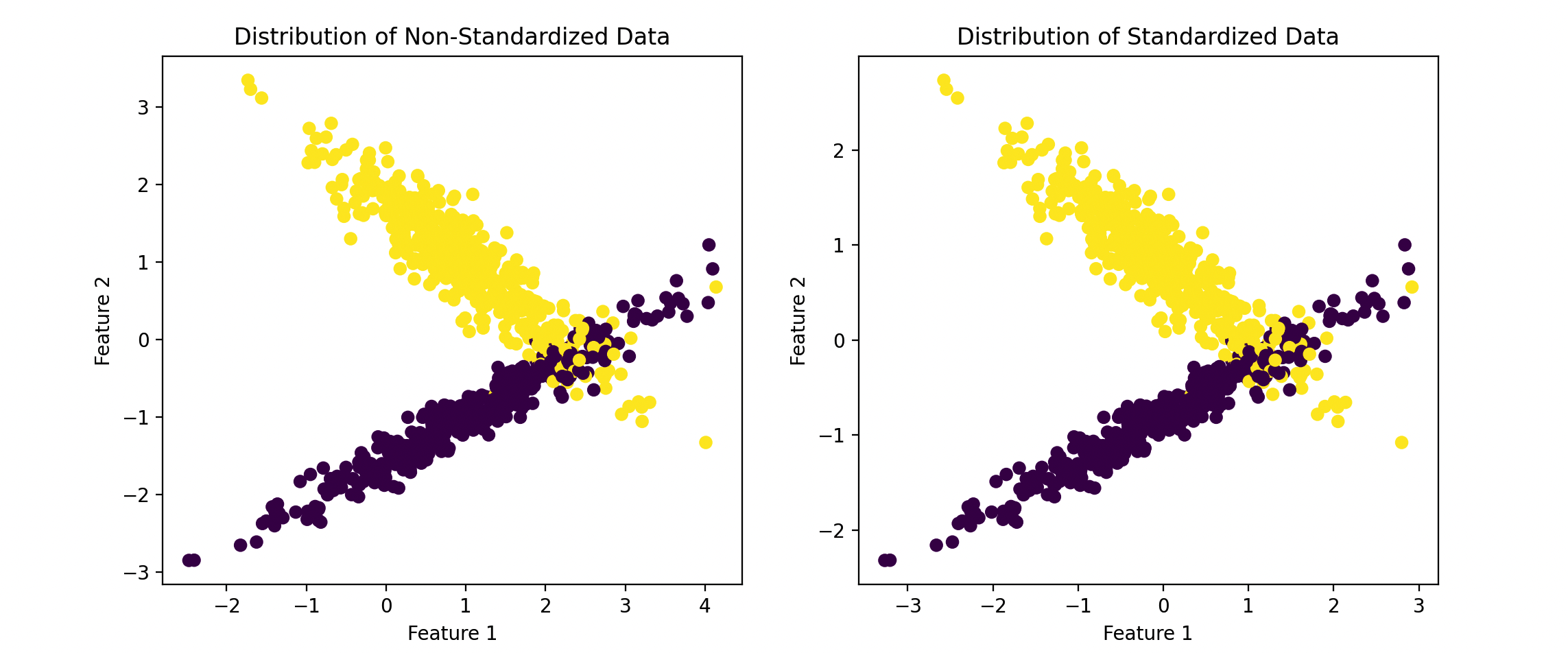
归一化与标准化的对比效果

标准化：更适用于数据没有明确边界的情况，可以处理具有异常值的特征。
归一化：适用于需要严格边界的情况，有助于缩小特征值的规模。

有机会的话，大家在后面的学习中，可以通过实际的模型和数据集，更加具体展示标准化和归一化对模型性能的不同影响，例如通过准确率、均方误差等指标来量化这些影响。另外，在实际应用中，选择哪种预处理方法取决于数据的特性和所使用的模型。

小数定标归一化

小数定标归一化在机器学习中常用来调整特征值的比例，使其落在一个较小的特定范围（通常是-1到1或者0到1）。该方法通过移动数据的小数点来实现归一化。小数点的移动位数依赖于属性值的最大绝对值。

该方法的核心是将数据缩放至其绝对值最大的那个数变为不大于1的数。例如，如果一个属性值的最大绝对值是123，则小数点需要移动三位，即每个值都除以1000。

公式推导

归一化公式为：

$ X_{\text{norm}} = \frac{X}{10^k} $

其中，$ X $ 是原始数据，$ X_{\text{norm}} $ 是归一化后的数据，$ k $ 是根据最大绝对值确定的小数点移动位数，计算方法为：

$ k = \lceil \log_{10} \max(\left| X \right|) \rceil $

这里，$ \lceil \cdot \rceil $ 表示向上取整，$ \log_{10} $ 表示以10为底的对数。

计算步骤

计算最大绝对值：找出数据集中所有数值的最大绝对值。
计算小数点移动位数 ( k )：使用上述公式计算 ( k )。
应用归一化公式：对数据集中的每个数值应用归一化公式。

案例代码

结合线性回归模型来演示小数定标归一化的效果。

代码中我们使用一个虚拟数据集来进行演示，并比较归一化前后的模型性能。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 生成虚拟数据集
np.random.seed(0)
X = np.random.rand(100, 1) * 100  # 随机生成0-100之间的数
y = 3 * X.squeeze() + 4 + np.random.randn(100)  # 线性关系加上噪声

# 定义小数定标归一化函数
def decimal_scaling_normalization(data):
    k = np.ceil(np.log10(np.max(np.abs(data))))
    return data / (10 ** k)

# 应用归一化
X_normalized = decimal_scaling_normalization(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
X_train_norm, X_test_norm = train_test_split(X_normalized, test_size=0.2, random_state=0)

# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)
model_norm = LinearRegression()
model_norm.fit(X_train_norm, y_train)

# 预测和评估
y_pred = model.predict(X_test)
y_pred_norm = model_norm.predict(X_test_norm)

mse_original = mean_squared_error(y_test, y_pred)
mse_normalized = mean_squared_error(y_test, y_pred_norm)

# 结果可视化
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red')
plt.title(f"Original Data (MSE: {mse_original:.2f})")

plt.subplot(1, 2, 2)
plt.scatter(X_test_norm, y_test, color='green')
plt.plot(X_test_norm, y_pred_norm, color='red')
plt.title(f"Normalized Data (MSE: {mse_normalized:.2f})")

plt.show()

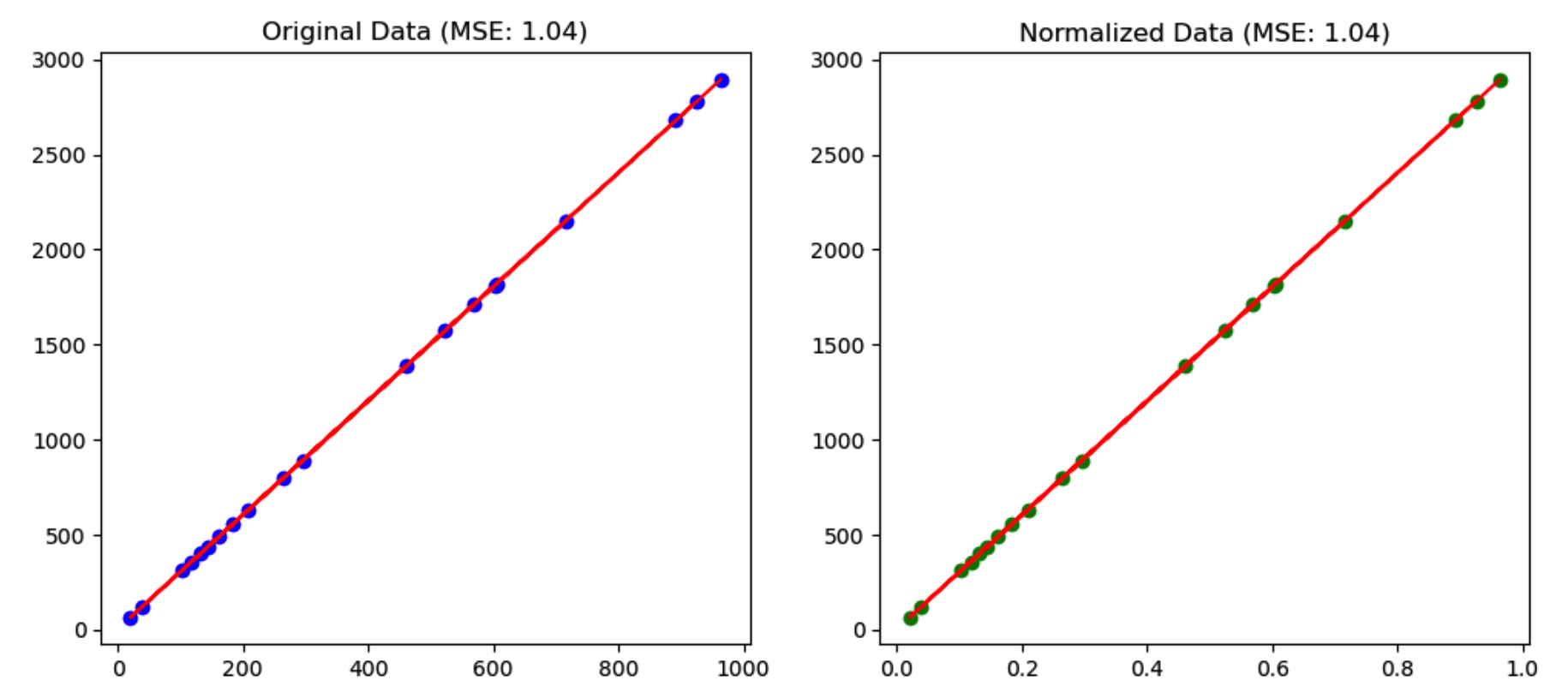
结果比较

上述代码中，我们首先生成了一个简单的线性关系数据集。然后，我们对这个数据集应用了小数定标归一化，并使用线性回归模型在归一化前后的数据上进行了训练和测试。

通过比较归一化前后的均方误差（MSE），我们可以看到归一化是否提升了模型的性能。同时，通过绘图，我们可以直观地看到归一化对模型预测结果的影响。通常，归一化会使模型训练更加稳定和快速，特别是在特征值范围差异较大的情况下。

均值归一化

均值归一化是一种常用的数据预处理方法，用于机器学习中的特征缩放。它的目的是调整特征数据的规模，使其在一个统一的范围内，通常是[-1, 1]。这样做可以加快学习算法的收敛速度，并提高算法的性能。

公式推导

均值归一化的公式可以表示为：

$$
x’ = \frac{x – \mu}{\sigma}
$$
其中，$ x’ $ 是归一化后的值，$ x $ 是原始数据，$ \mu $ 是原始数据的均值，$ \sigma $ 是原始数据的标准差。

计算步骤

计算均值和标准差：对于每个特征，计算其所有数据点的均值和标准差。
应用归一化公式：使用上述公式对每个特征的每个数据点进行归一化处理。

案例代码

结合KNN，在算法中应用均值归一化。同时使用一个虚拟数据集来演示这一过程，并且比较归一化前后的效果。

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# 生成虚拟数据集
np.random.seed(0)
X = np.random.rand(1000, 2)  # 1000个样本，每个样本2个特征
y = np.random.randint(0, 2, 1000)  # 生成0和1的标签

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 不使用归一化
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
predictions = knn.predict(X_test)
accuracy_without_normalization = accuracy_score(y_test, predictions)

# 使用均值归一化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

knn.fit(X_train_scaled, y_train)
predictions = knn.predict(X_test_scaled)
accuracy_with_normalization = accuracy_score(y_test, predictions)

# 可视化比较结果
plt.bar(['Without Normalization', 'With Normalization'], [accuracy_without_normalization, accuracy_with_normalization])
plt.ylabel('Accuracy')
plt.title('Comparison of KNN Accuracy with and without Mean Normalization')
plt.show()

使用KNN算法分别在未归一化的数据和经过均值归一化的数据上进行训练和测试，并比较了两种情况下的准确率。

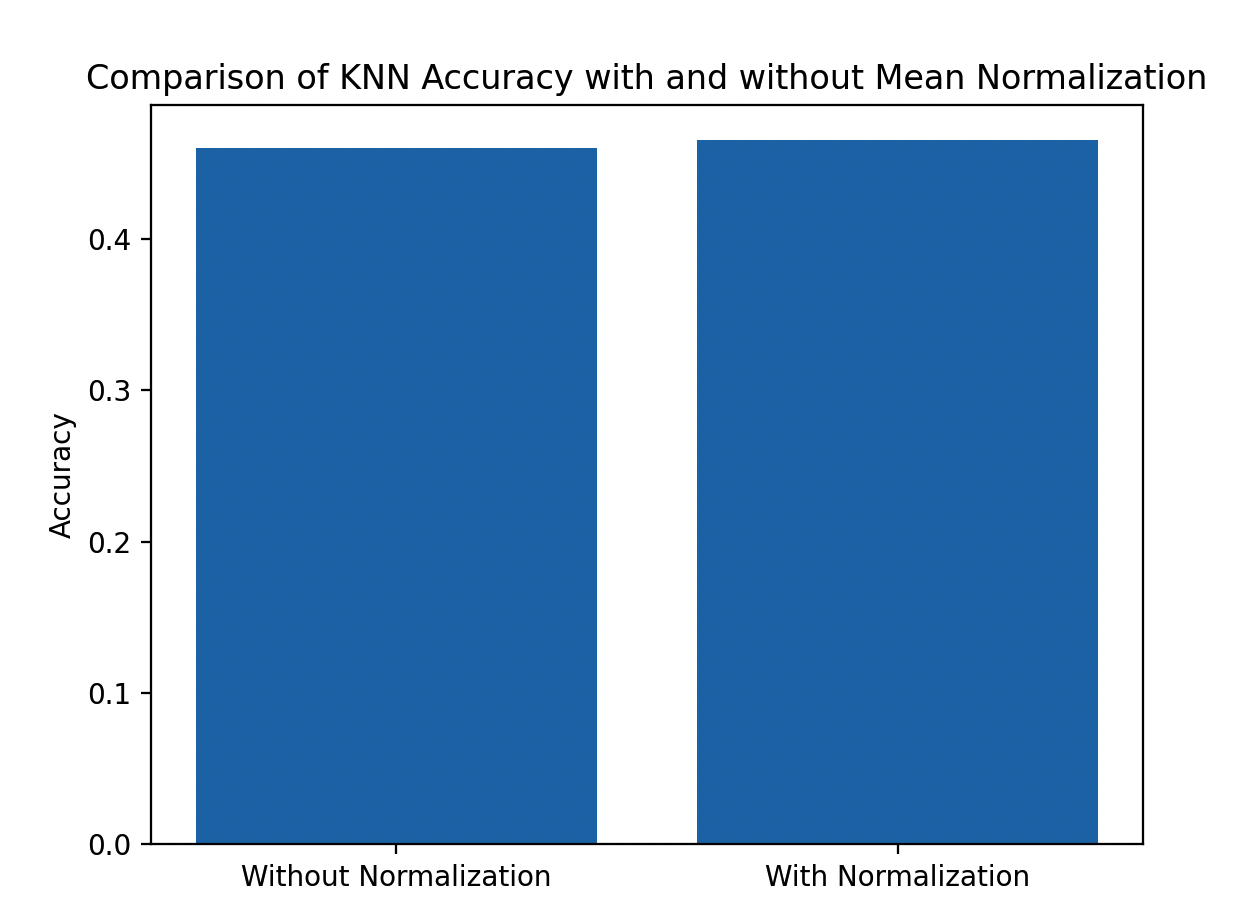
归一化前后的对比效果

收敛速度：归一化后，特征值的规模统一，有助于加速学习算法的收敛。
算法性能：特征归一化可以提高算法性能，特别是在使用基于距离的算法（如KNN）时更为明显。

最后，通过绘制的柱状图可以直观地比较归一化前后KNN算法的准确率，从而验证均值归一化对模型性能的影响。

单位长度归一化

单位长度归一化是一种常见的数据预处理技术，用于机器学习中的特征缩放。其目的是调整数据集中特征的尺度，使每个特征的值都按其长度进行缩放，从而具有单位长度。

算法原理

单位长度归一化的基本原理是将每个特征向量调整为单位长度。这通常通过将每个特征向量除以其欧几里得范数（即向量的长度）来实现。

公式推导

考虑一个特征向量 $ \mathbf{x} = (x_1, x_2, \ldots, x_n) $，其单位长度归一化的向量为 $ \mathbf{x’} $，其中：

$$
\mathbf{x’} = \frac{\mathbf{x}}{\| \mathbf{x} \|}
$$
其中，$ \| \mathbf{x} \| $ 是 $ \mathbf{x} $ 的欧几里得范数，计算为：

$$
\| \mathbf{x} \| = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}
$$
因此，归一化后的每个元素 $ x’_i $ 为：

$$
x’_i = \frac{x_i}{\sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}}
$$

计算步骤

计算原始特征向量的欧几里得范数。
将每个特征值除以该范数。

案例代码

结合线性回归，并使用虚拟数据集进行代码的编写。

为了更丰富地展示单位长度归一化对模型性能的影响，我们可以增加一些额外的可视化，例如展示预测误差的分布和特征值的分布对比。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 创建虚拟数据集
np.random.seed(0)
X = np.random.rand(100, 3)  # 100个样本，3个特征
y = X @ np.array([1.5, -2.0, 1.0]) + np.random.randn(100) * 0.5  # 目标变量

# 单位长度归一化
norm_X = X / np.linalg.norm(X, axis=1, keepdims=True)

# 分割数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
norm_X_train, norm_X_test = train_test_split(norm_X, test_size=0.2, random_state=42)

# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)
norm_model = LinearRegression()
norm_model.fit(norm_X_train, y_train)

# 预测和评估
y_pred = model.predict(X_test)
norm_y_pred = norm_model.predict(norm_X_test)

mse = mean_squared_error(y_test, y_pred)
norm_mse = mean_squared_error(y_test, norm_y_pred)

# 结果比较
print("MSE without normalization:", mse)
print("MSE with unit length normalization:", norm_mse)

# 绘制结果
plt.figure(figsize=(18, 6))

# 预测值与实际值对比
plt.subplot(1, 3, 1)
plt.scatter(y_test, y_pred, label='Without Normalization')
plt.scatter(y_test, norm_y_pred, color='r', label='With Normalization')
plt.title("Predictions vs True Values")
plt.xlabel("True Values")
plt.ylabel("Predictions")
plt.legend()

# 预测误差分布
plt.subplot(1, 3, 2)
plt.hist(y_test - y_pred, bins=15, alpha=0.7, label='Without Normalization')
plt.hist(y_test - norm_y_pred, bins=15, alpha=0.7, color='r', label='With Normalization')
plt.title("Prediction Error Distribution")
plt.xlabel("Prediction Error")
plt.ylabel("Frequency")
plt.legend()

# 特征分布对比
plt.subplot(1, 3, 3)
for i in range(X.shape[1]):
    plt.hist(X[:, i], bins=15, alpha=0.5, label=f'Feature {i+1} Original')
    plt.hist(norm_X[:, i], bins=15, alpha=0.5, color='r', label=f'Feature {i+1} Normalized')
plt.title("Feature Distributions")
plt.xlabel("Feature Value")
plt.ylabel("Frequency")
plt.legend()

plt.tight_layout()
plt.show()

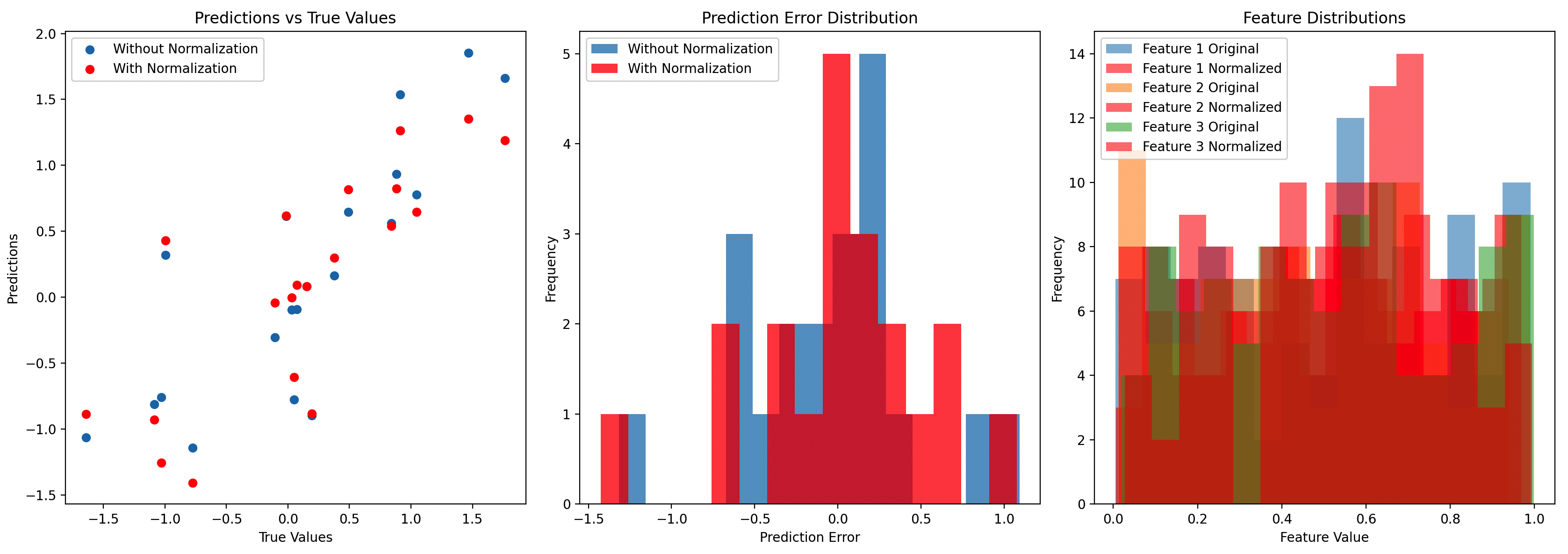
上述代码将创建三个图表：

预测值与实际值对比：展示了归一化前后模型预测值与实际值的关系。
预测误差分布：通过直方图展示了归一化前后预测误差的分布情况，有助于理解模型性能的提升。
特征分布对比：比较了原始数据和经过单位长度归一化后的特征值分布，以展示归一化对数据的影响。

这些图表提供了更全面的视角来观察数据预处理对模型性能的影响。

声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。

昨天，我看到社群里，大家在讨论一个问题：归一化。

最小-最大归一化

公式说明

计算步骤

案例代码

归一化前后对比

标准化

公式推导

计算步骤

案例代码

归一化与标准化的对比效果

小数定标归一化

公式推导

计算步骤

案例代码

结果比较

均值归一化

公式推导

计算步骤

案例代码

归一化前后的对比效果

单位长度归一化

算法原理

公式推导

计算步骤

案例代码

发表回复取消回复

原创精华

机器学习核心内容

大数据相关

昨天，我看到社群里，大家在讨论一个问题：归一化。

最小-最大归一化

公式说明

计算步骤

案例代码

归一化前后对比

标准化

公式推导

计算步骤

案例代码

归一化与标准化的对比效果

小数定标归一化

公式推导

计算步骤

案例代码

结果比较

均值归一化

公式推导

计算步骤

案例代码

归一化前后的对比效果

单位长度归一化

算法原理

公式推导

计算步骤

案例代码

发表回复 取消回复

发表回复取消回复