案例介绍
在这个案例中,我们将使用DBSCAN算法对波士顿房屋数据进行聚类分析。DBSCAN是一种密度聚类算法,它可以发现有意义的数据聚类并标记离群点。
算法原理
DBSCAN算法基于以下两个关键概念:核心对象和密度可达。
- 核心对象:给定一个半径为 $\epsilon$ 的邻域,如果该邻域内至少存在 MinPts 个数据点,则称这个数据点为核心对象。
- 密度可达:如果一个数据点可以通过一系列的邻域跳转到核心对象,则该数据点与核心对象密度可达。
在算法中,我们定义了三个类型的数据点:
- 核心对象:在给定半径 $\epsilon$ 内至少存在 MinPts 个数据点的数据点。
- 边界点:不是核心对象,但距离某个核心对象的距离在 $\epsilon$ 范围内的数据点。
- 噪声点:既不是核心对象,也不是边界点的数据点。
DBSCAN算法的基本思想是通过不断扩展核心对象的邻域,找到密度可达的数据点,从而形成一个聚类。
公式推导
在推导公式之前,我们定义几个符号:
– $D$ 是数据集,包含 $n$ 个数据点:$D = \{p_1, p_2, …, p_n\}$;
– 对于每个数据点 $p_i$,定义其邻域为 $N(p_i) = \{p_j \in D | dist(p_i, p_j) \leq \epsilon\}$;
– 数据点 $p_i$ 的密度为 $density(p_i) = |N(p_i)|$;
DBSCAN算法中的距离度量通常使用欧氏距离,即 $dist(p_i, p_j) = \sqrt{\sum_{k=1}^{m}(p_{ik}-p_{jk})^2}$。
给定以上定义,我们可以推导出以下公式:
1. 核心对象(Core Object)的定义:
- 对于数据点 $p_i$,如果 $density(p_i) geq MinPts$,则 $p_i$ 是核心对象。
2. 密度直达(Density Directly Reachable):
- 对于数据点 $p_i$ 和 $p_j$,如果 $p_j in N(p_i)$,且 $density(p_j) geq MinPts$,则 $p_i$ 和 $p_j$ 密度直达。
3. 密度可达(Density Reachable):
- 对于数据点 $p_i$ 和 $p_j$,如果存在一系列数据点 $p_1, p_2, …, p_n$ 使得 $p_1 = p_i$,$p_n = p_j$,且 $p_{k+1}$ 密度直达 $p_k$,则 $p_i$ 和 $p_j$ 密度可达。
4. 密度相连(Density Connected):
- 对于数据点 $p_i$ 和 $p_j$,如果存在一个数据点 $p_k$,使得 $p_i$ 和 $p_j$ 密度可达,并且 $p_i$ 和 $p_j$ 密度直达 $p_k$,则 $p_i$ 和 $p_j$ 密度相连。
基于以上定义,我们可以用图的形式表示密度相连的数据点之间的关系,从而进行聚类分析。
数据集
在这个案例中,我们将使用波士顿房屋数据集。该数据集包含了506个房屋样本,每个样本有13个特征变量(比如:房间数、犯罪率等)和1个目标变量(房屋价格)。我们将根据这13个特征对房屋进行聚类分析,试图找到有着相似特征的房屋聚类。
你可以使用 sklearn.datasets 中的 load_boston() 函数来进行数据集的载入。
from sklearn.datasets import load_boston
# 载入波士顿房屋数据集
boston = load_boston()
# 获取特征数据
X = boston.data
print(X.shape) # 输出 (506, 13)计算步骤
- 载入数据集
- 标准化数据(如果需要)
- 设定 DBSCAN 相关参数:$epsilon$ 和 MinPts
- 执行 DBSCAN 算法
- 可视化聚类结果
Python代码示例
下面是一个使用 DBSCAN 对波士顿房屋数据进行聚类分析的完整Python代码示例,我们将使用 Scikit-learn 中的 DBSCAN 类。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN
# 载入波士顿房屋数据集
boston = load_boston()
X = boston.data
# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 设定 DBSCAN 相关参数
epsilon = 2
min_samples = 5
# 执行 DBSCAN 算法
dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
dbscan.fit(X_scaled)
# 获取每个数据点的类别标签
labels = dbscan.labels_
# 聚类结果可视化
unique_labels = np.unique(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for label, color in zip(unique_labels, colors):
if label == -1:
# 噪声点为黑色
color = [0, 0, 0, 1]
# 属于该类别的数据点的索引
class_member_mask = (labels == label)
xy = X_scaled[class_member_mask]
# 绘制当前类别的数据点
plt.scatter(xy[:, 0], xy[:, 1], s=50, c=[color], marker='o', alpha=0.5)
plt.title('DBSCAN Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()在上述代码中,我们首先对数据进行了标准化处理,然后设定了 DBSCAN 的参数值($epsilon=2$,$MinPts=5$)。然后,使用 DBSCAN 类对数据进行聚类分析,并获取了每个数据点的类别标签。最后,我们使用散点图将聚类结果可视化。其中,不同颜色代表不同的聚类簇,黑色代表噪声点。

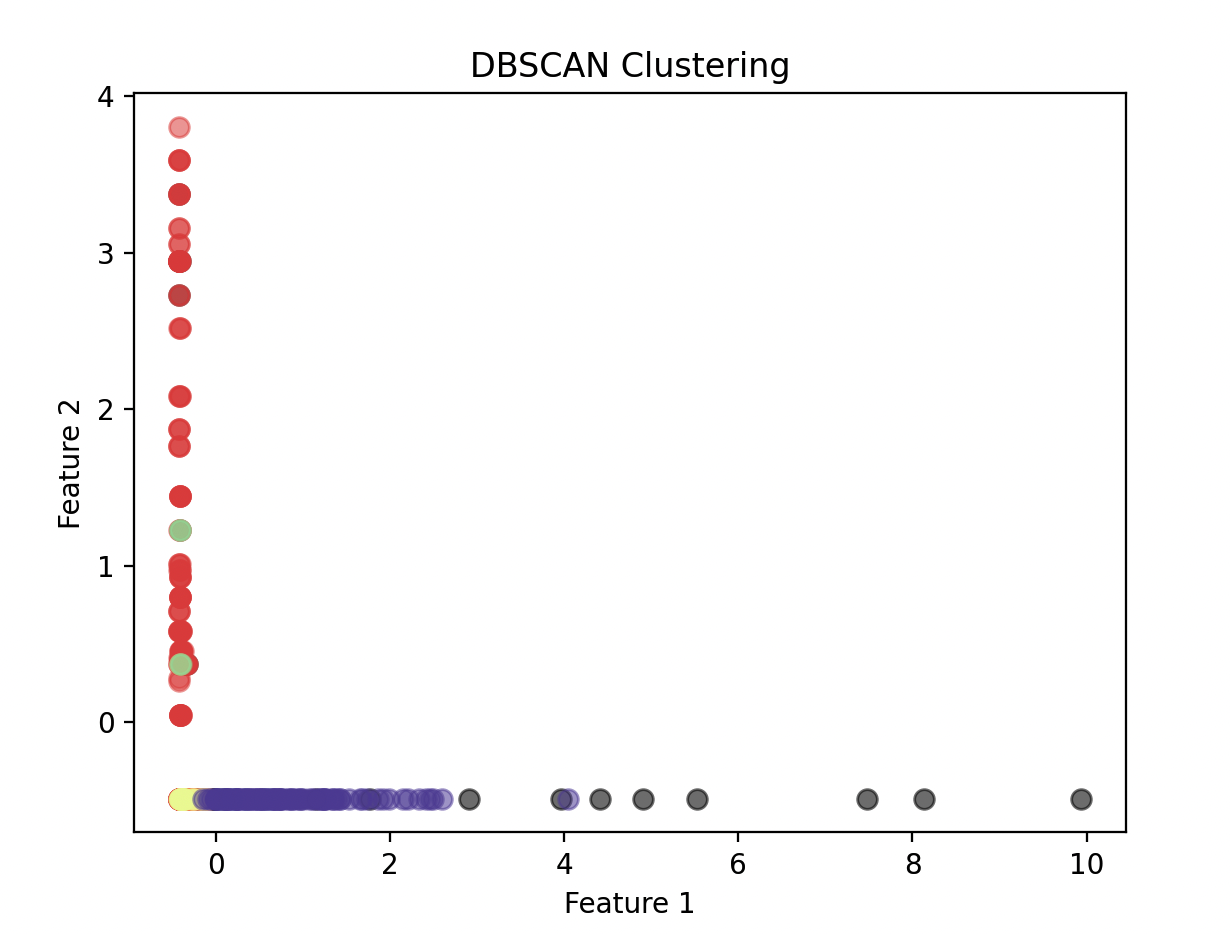
代码细节解释
- 首先导入必要的库:
numpy、matplotlib.pyplot、sklearn.datasets、sklearn.preprocessing和sklearn.cluster。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import DBSCAN- 载入波士顿房屋数据集,并获取特征数据。
boston = load_boston()
X = boston.data- 标准化数据。由于不同的特征变量具有不同的尺度,为了避免这种尺度差异对聚类结果的影响,我们使用
StandardScaler对数据进行标准化处理。
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)- 设定 DBSCAN 的参数:$epsilon$ 和 MinPts。
epsilon = 2
min_samples = 5- 执行 DBSCAN 算法。通过调用
DBSCAN()函数并传入相应的参数,我们创建了一个 DBSCAN 对象,并使用fit()方法对数据进行聚类分析。
dbscan = DBSCAN(eps=epsilon, min_samples=min_samples)
dbscan.fit(X_scaled)- 获取每个数据点的类别标签。
labels = dbscan.labels_- 可视化聚类结果。我们首先获取每个数据点的类别标签,并根据不同的标签设定不同的颜色。然后,使用
scatter()函数将聚类结果可视化。在这里,我们使用了两个特征变量进行可视化,你可以根据实际需求选择不同的特征。
# 获取每个类别
unique_labels = np.unique(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for label, color in zip(unique_labels, colors):
if label == -1:
# 噪声点为黑色
color = [0, 0, 0, 1]
# 属于该类别的数据点的索引
class_member_mask = (labels == label)
xy = X_scaled[class_member_mask]
# 绘制当前类别的数据点
plt.scatter(xy[:, 0], xy[:, 1], s=50, c=[color], marker='o', alpha=0.5)
plt.title('DBSCAN Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()在上面的代码中,我们循环遍历每个类别的数据点,并分别绘制散点图。噪声点使用黑色表示,而其他类别则使用根据类别数量而均匀分布的颜色进行表示。
