哈喽,我是cos大壮~
这几天一部分社群确实活跃了起来,今儿上午有一些大咖在一起聊高斯混合模型~
趁着这个热度,我这边也来聊聊,不熟悉的小伙伴,可以一起学习起来!
Gaussian Mixture Model (GMM) 是一种强大的概率模型,用于表示由多个高斯分布组成的复杂数据集。
在GMM中,每个数据点被认为是由多个高斯分布之一产生的,而这些高斯分布代表数据中的不同子群体或簇。
咱们先来大概列举一些GMM的关键特点:
- 混合高斯分布:GMM假设数据是由几个高斯分布混合而成的。每个高斯分布称为模型的一个“组件”或“簇”,具有自己的均值(决定中心)和协方差(决定形状和扩散程度)。
- 概率模型:与传统的聚类方法(如K-means)不同,GMM为软聚类提供了框架。这意味着每个数据点都以一定的概率属于每个簇,而不是被硬性划分到某个簇中。
- 参数估计:GMM通常使用一种称为“期望最大化”(EM)的算法来估计其参数。EM算法通过迭代过程逐渐逼近最优解,交替执行计算每个数据点属于每个簇的概率(E步骤),以及更新簇的参数(M步骤)。
- 应用广泛:由于其灵活性和强大的建模能力,GMM被广泛应用于聚类分析、密度估计、模式识别等领域。
- 选择组件数:在实际应用中,选择合适的簇(组件)数量是关键,这通常需要基于数据的特性和目标任务来决定。
GMM尤其是在聚类分析、密度估计和模式识别等领域发挥其明显的特征。这些特性使其成为分析和建模复杂数据集的一个非常非常强大的工具。
有了这个大概的印象,咱们继续深度探讨 GMM 的一些基本原理~
一些概念
高斯分布
定义与特性
- 高斯分布,又称正态分布,是连续概率分布的一种。
- 它由两个参数定义:均值(μ)和方差(σ²)。均值决定了分布的中心位置,而方差则描述了数据点围绕均值的分散程度。
- 在一维空间中,高斯分布的概率密度函数呈钟形,对称于均值。
- 在多维空间中,高斯分布由均值向量和协方差矩阵定义。均值向量指出了分布中心的位置,而协方差矩阵则描述了各维度间的关系和分布的形状。
多维高斯分布
- 在多维空间中,高斯分布的概率密度函数更为复杂,因为它涉及到各维度之间的协方差。
- 协方差矩阵不仅告诉我们每个维度上的方差,还告诉我们不同维度之间的相关性。
混合模型
混合模型的概念
- 混合模型假设数据是由多个简单模型(如高斯分布)的组合生成的。
- 在GMM中,这些简单模型是高斯分布,每个高斯分布被视为数据中的一个“子群体”或“簇”。
高斯混合模型的构成
- GMM将数据集视为若干个高斯分布的叠加。
- 每个高斯分布代表数据中的一个子群体,具有自己的均值(表示群体中心)和协方差(表示群体的形状和大小)。
模型的灵活性:
- 由于高斯分布本身的灵活性以及多个分布的组合,GMM能够适应各种复杂的数据分布,这使得它成为一种强大的聚类和密度估计工具。
混合系数
混合系数的作用:
- 在GMM中,每个高斯分布有一个对应的“混合系数”,它表示该高斯分布在整个数据集中所占的比重。
- 这些系数表明了各个子群体在总体数据中的相对重要性。
约束条件:
- 所有混合系数的总和必须等于1(即 $ sum_{k=1}^{K} pi_k = 1 $),确保总概率密度函数是合法的概率分布。
通过结合多个高斯分布和相应的混合系数,GMM能够表示出比单个高斯分布更复杂的数据结构。这种方法既考虑了数据中的多样性(通过多个高斯分布)又保持了模型的统一性(通过概率的框架)。
接下来,咱们从公式方面进行阐述~
$ K $ 个高斯分布组成的GMM
一个由 $ K $ 个高斯分布组成的GMM可以表示为:
$ K $ 个高斯分布组成的GMM
一个由 $ K $ 个高斯分布组成的GMM可以表示为:
$$
p(x) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x | \mu_k, \Sigma_k)
$$
– $ \pi_k $:第 $ k $ 个高斯分布的混合系数。
– $ \mathcal{N}(x | \mu_k, \Sigma_k) $:表示具有均值 $ \mu_k $ 和协方差矩阵 $ \Sigma_k $ 的高斯分布的概率密度函数。
高斯分布的概率密度函数
$$
\mathcal{N}(x | \mu_k, \Sigma_k) = \frac{1}{(2\pi)^{n/2}|\Sigma_k|^{1/2}} \exp \left( -\frac{1}{2} (x – \mu_k)^T \Sigma_k^{-1} (x – \mu_k) \right)
$$
– $ \mu_k $:均值向量。
– $ \Sigma_k $:协方差矩阵。
– $(2\pi)^{n/2}$ 和 $|\Sigma_k|^{1/2}$:归一化因子。
– 指数部分:数据点 $ x $ 偏离均值 $ \mu_k$ 的程度。
参数估计 – 期望最大化(EM)算法
E步骤(期望步骤):
- 估计每个数据点属于每个高斯分布的概率。
- 计算责任值 $ \gamma(z_{nk}) $,表示数据点 $ n $ 属于簇 $ k $ 的概率。
M步骤(最大化步骤):
– 使用责任值来重新估计高斯分布的参数。
– 更新公式为:
$ \mu_k^{new} = \frac{1}{N_k} \sum_{n=1}^{N} \gamma(z_{nk}) x_n $
$ \Sigma_k^{new} = \frac{1}{N_k} \sum_{n=1}^{N} \gamma(z_{nk}) (x_n – \mu_k^{new})(x_n – \mu_k^{new})^T $
$ \pi_k^{new} = \frac{N_k}{N} $
– $ N_k = \sum_{n=1}^{N} \gamma(z_{nk}) $:归属于簇 $ k $ 的数据点的有效数量。
算法流程
- 初始化参数:随机选择均值、协方差和混合系数。
- 迭代执行E步和M步:直到满足收敛条件(如参数变化小于某个阈值或达到最大迭代次数)。
模型选择和评估
- 选择正确的簇数量对GMM至关重要,通常通过BIC或AIC标准来评估。
- GMM适用于软聚类和密度估计。
总之,GMM是通过结合多个高斯分布提供了一种模拟复杂数据分布的强大方法,但其效果高度依赖于初始化和所选簇的数量。
这使得GMM在数据科学和统计建模中成为了一个非常有用的工具。
一个案例
下面这段代码,摘取自sklearn官网,代码展示了如何使用不同的初始化方法来评估 Gaussian Mixture Models (GMM) 的性能。
大家可以细致的了解一下,我将代码中重要的部分,标注了详细的注释。
from timeit import default_timer as timer
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets._samples_generator import make_blobs
from sklearn.mixture import GaussianMixture
from sklearn.utils.extmath import row_norms
# 生成模拟数据
X, y_true = make_blobs(n_samples=4000, centers=4, cluster_std=0.60, random_state=0)
X = X[:, ::-1] # 反转特征顺序
# 初始化一些参数
n_samples = 4000
n_components = 4
x_squared_norms = row_norms(X, squared=True) # 计算数据点的平方范数
# 定义函数以获取GMM的初始均值
def get_initial_means(X, init_params, r):
# 使用GaussianMixture获取初始化均值
gmm = GaussianMixture(
n_components=4, init_params=init_params, tol=1e-9, max_iter=0, random_state=r
).fit(X)
return gmm.means_
# 定义初始化方法和相关配置
methods = ["kmeans", "random_from_data", "k-means++", "random"]
colors = ["navy", "turquoise", "cornflowerblue", "darkorange"]
times_init = {} # 存储初始化时间
relative_times = {} # 存储相对于第一种方法的初始化时间
# 设置绘图
plt.figure(figsize=(4 * len(methods) // 2, 6))
plt.subplots_adjust(bottom=0.1, top=0.9, hspace=0.15, wspace=0.05, left=0.05, right=0.95)
# 对于每种初始化方法
for n, method in enumerate(methods):
r = np.random.RandomState(seed=1234)
plt.subplot(2, len(methods) // 2, n + 1)
# 记录初始化时间
start = timer()
ini = get_initial_means(X, method, r)
end = timer()
init_time = end - start
# 应用GaussianMixture模型
gmm = GaussianMixture(
n_components=4, means_init=ini, tol=1e-9, max_iter=2000, random_state=r
).fit(X)
# 保存和计算时间
times_init[method] = init_time
relative_times[method] = times_init[method] / times_init[methods[0]]
# 绘制GMM的结果
for i, color in enumerate(colors):
data = X[gmm.predict(X) == i]
plt.scatter(data[:, 0], data[:, 1], color=color, marker="x")
plt.scatter(ini[:, 0], ini[:, 1], s=75, marker="D", c="orange", lw=1.5, edgecolors="black")
plt.xticks(())
plt.yticks(())
plt.title(method, loc="left", fontsize=12)
plt.title("Iter %i | Init Time %.2fx" % (gmm.n_iter_, relative_times[method]), loc="right", fontsize=10)
# 显示绘制的图形
plt.suptitle("GMM iterations and relative time taken to initialize")
plt.show()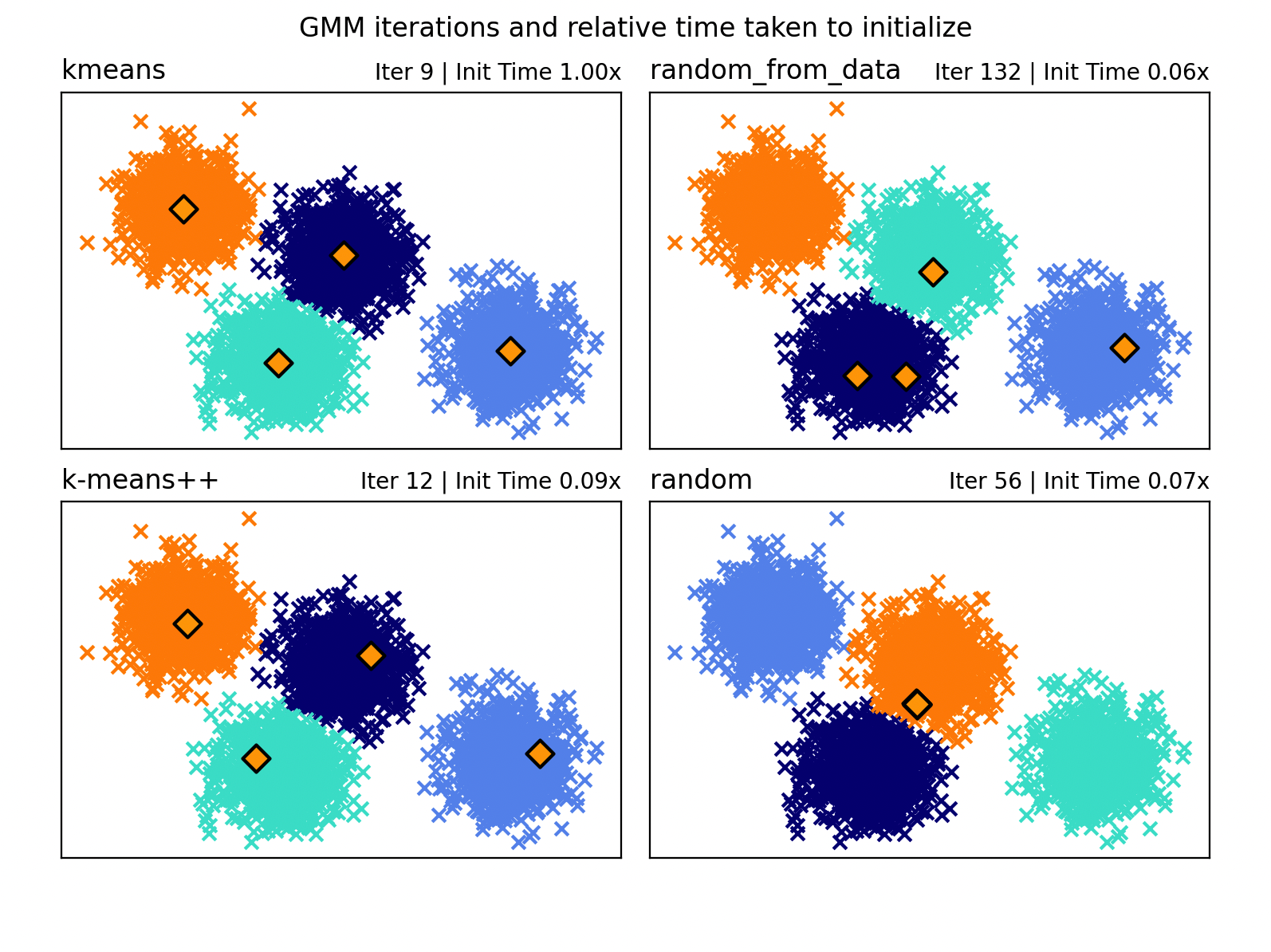
这段代码的量还是不小,下面对于一些关键点,再详细的说说~
- 数据生成:
- 使用
make_blobs从 sklearn 库生成了一组模拟数据。这些数据由 4000 个样本点组成,分布在 4 个不同的中心,每个中心具有 0.60 的标准差。这些数据用于后续的 GMM 聚类。
- 使用
- 初始化配置:
- 定义了样本数量(4000)和组件数(4)。
- 计算了数据点的平方范数,这在某些初始化方法中可能会用到。
- 定义初始化均值函数:
- 编写了一个函数
get_initial_means,该函数使用GaussianMixture类从 sklearn 库初始化 GMM,并返回根据指定的初始化方法得到的均值。这个函数对于比较不同初始化方法的影响至关重要。
- 编写了一个函数
- 不同初始化方法的应用:
- 选择了四种不同的初始化方法:
"kmeans","random_from_data","k-means++", 和"random"。这些方法代表了从标准的 K-means 到完全随机的不同方式来初始化 GMM 的均值。
- 选择了四种不同的初始化方法:
- 性能评估与可视化:
- 对每种初始化方法,代码记录了初始化所需的时间,并使用 GMM 对数据进行了拟合。
- 计算了相对于第一种方法(”kmeans”)的相对初始化时间。
- 通过
matplotlib生成了一个包含多个子图的图形,每个子图展示了使用一种初始化方法的 GMM 聚类结果。聚类中心用橙色菱形标记,不同的颜色代表不同的聚类。
- 结果展示:
- 在图形的标题中显示了每种方法的迭代次数和相对于第一种方法的初始化时间。
- 最终,展示了一个整体的图表,其中包括了所有初始化方法的聚类结果和性能比较。
上面代码用不同初始化方法演示了如何影响 GMM 的聚类效果和计算效率,最后通过可视化的方式,使这些差异一目了然。
ok,这就是今天想要和大家分享的内容,主要是关于 GMM 的原理和实践。
